Tower of Hanoi: It's a puzzle game with three towers and disks; transferring all the disks from the source tower to the destination tower seems easy, but there are some rules we need to follow to play this game. Please check the rules below.

Rules:

• Only transfer one disk at a time

• A smaller disk is always kept on a larger disk

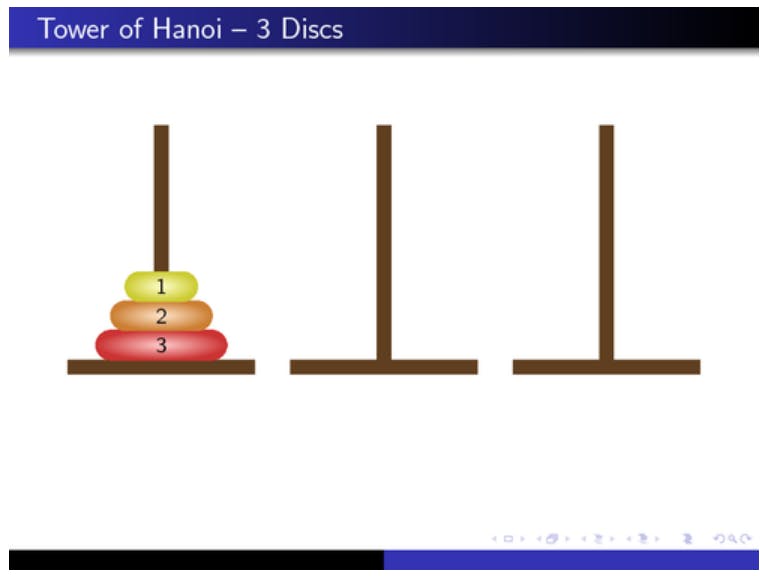
Now assume the first tower stack with three disks is the source (S), the middle one is the helper(H), and the disk at the end is the destination(D)

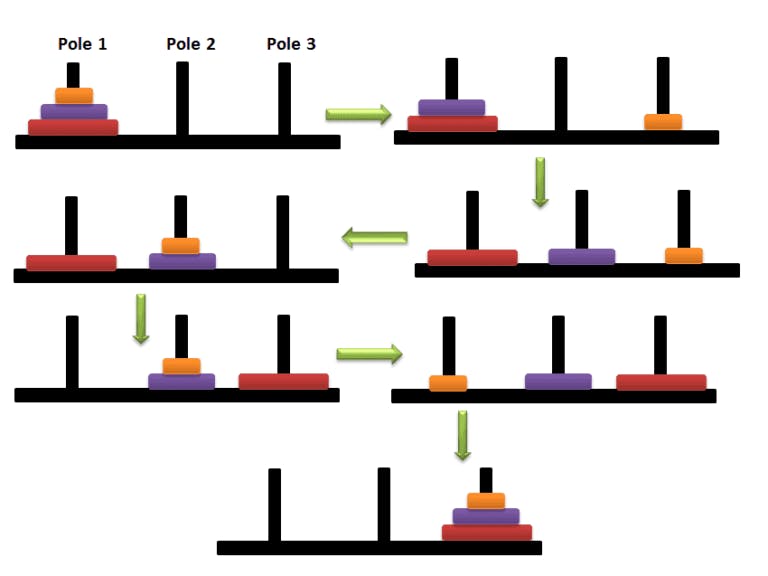
Let's take different possible events for other disks.

• Point 1: Only one disk: we can directly transfer it to the destination with one step

• Point 2: For two disks, we need to transfer the first disk to the helper, then to 2nd disk to the destination, and now transfer 1st disk to the destination from the helper, so this process takes three steps to reach the goal.

• Point 3: For three disks: we somehow need to take the last disk to the destination, but we have two disks stacked there; for now, we can ignore the last disk, and for those disks, we have the same condition as 2nd point for that destination become helper and helper become a destination which would take three steps and now we have one disk left on the source so we can transfer it to the destination which would take a step like first point. Now we have two disks on the helper, which is the same situation as 2nd point; now the source is the helper, and it will take the same three-step. This process takes 3 + 1 + 3 = 7 steps.

From the third point, we can see that the whole process is repeated, just the tower changed, so we can use recursion to solve the problem; let's take the different cases to code these.

Base case: If one disk is left at the source, we directly transfer it to the destination.

Recursive case (Transfer n-1 disk to a helper as a destination from source): If there is more than one disk in the source, then we have to take the (n-1) disk to the helper; Thats the only way we can transfer the last disk to the destination to reach this position we need to make helper destination and destination helper for (n-1) disk.

# here destination become helper and helper become destination 
towerOfHanoi(n-1,src,dest,helper) # recursive function for n-1 disk

Recursive case (Transfer n-1 disk to a destination from a helper as a source): Now same process, we need to take sources as helper and helper as a source to transfer (n-1) disks to the destination.

 # here source become helper and helper become source   
towerOfHanoi(n-1,helper,src,dest) # recursive function for n-1 disk

Code:

def towerOfHanoi(n:int,src:str,helper:str,dest:str):
    if n == 1:
        print(f"transfer disk {n} from {src} to {dest}")
        return
    towerOfHanoi(n-1,src,dest,helper)
    print(f"transfer disk {n} from {src} to {dest}")
    towerOfHanoi(n-1,helper,src,dest)
n = 3
towerOfHanoi(n,"S","H","D")

Result: For n=3 (Here S: Source, H: Helper, D: Destination):

transfer disk 1 from S to D
transfer disk 2 from S to H
transfer disk 1 from D to H
transfer disk 3 from S to D
transfer disk 1 from H to S
transfer disk 2 from H to D
transfer disk 1 from S to D

Time Complexity:

For example, n = 5, here are two recursive functions, so there will be two function calls for each recursive function except the first call.

• for n= 5, one function call -> 1

• for n= 4, 2 * previous call -> 2

• for n= 3, 2 * previous call -> 2²

• for n = 2, 2 * previous call ->2³

• for n =1, 2 * previous call -> 2⁴

• Similarly, for n-1, it will take 2^n-1 calls which is the worst case, so our time complexity is O(2^n-1).

The Time Complexity of this algorithm is O(2ⁿ).

The fascinating thing about this algorithm:

This algorithm is similar to a binary number.

• 0-> 1 -> roll back -> 10 -> 11-> roll back -> 100-> 101-> 111 -> roll back ->1000-> ...

• Please check this link to understand more about this concept: https://www.youtube.com/watch?v=2SUvWfNJSsM

More Content:

Video: Link, In-depth video: Link

References:

• Image-2

• Image-1